[Computer vision] Efficient adaptive non-maximal suppression

Link: https://www.researchgate.net/publication/323388062_Efficient_adaptive_non-maximal_suppression_algorithms_for_homogeneous_spatial_keypoint_distribution

Github: https://github.com/BAILOOL/ANMS-Codes

 

SLAM을 위해 이미지에서 keypoint detection을 하게 되면 알고리즘에 의해 주로 같은 위치에서 여러 번 중복 검출이 되는 현상이 발생한다.

 

이렇게 중복 검출된 keypoint들은 오히려 SLAM의 성능을 저하시키는 요인이 된다.

(In terms of memory, processing time, noise, etc.)

 

그래서 non-maximum suppression과 같은 technique들을 사용해서 최적의 keypoint 위치를 하나만 빼고 제거한다.

해당 논문에서는 keypoint 검출 이후의 ANMS를 효율적이고 빠르게 할 수 있는 방법을 제안한다. 

기존의 ANMS는 computational cost가 높아서 실제로 많이 적용이 되지 않았다. 

논문에서는 3가지 approach를 제안한다. 

• Range Tree ANMS (RT ANMS)
• K-d Tree ANMS (K-dT ANMS)
• Suppression via Square Covering  (SSC)

 

이 포스팅에서는 SSC에 대해 살펴본다.

 

---

 

Algorithm

 

SSC algorithm

- 여기서 $w = a_h$ 이다.

($a_h$는 뒤에 이어서 설명한다)

 

 

Overview

 

먼저 keypoint detector에 의해서 뽑힌 점들의 vector를 코너성분이 강한 정도에 따라 내림차순으로 정렬한다. 

 

이 vector $P_in$은 그 후에 iterative하게 중복 점을 제거하여 keypoint의 개수를 줄이고, 고르게 분포된 vector로 만드는 과정을 반복하여 $P_out$이 된다. 

 

이 때 $P_out$의 개수는 사용자가 지정할 수 있는 값이다. 

 

Adaptive search range of size $w$ 는 최종 $P_out$의 개수가 사용자가 설정한 값에 비슷해질 때까지(via thresholding) 지속적으로 조정된다. 

 

 

 

Initializing Binary Search Boundaries

 

Clustered 되지 않고 Homogeneous하게 분포된 $m$개의 search boundary를 정의한다.

그러기 위해서 먼저 이미지를 사각형으로 덮는다. 

 

이 때 사각형은 한 변의 길이가 $2a_h$이고, 각 사각형의 중점은 최소한 이웃한 사각형과 $a_h+1$ 이상의 거리만큼은 떨어져 있어야 한다. 

 

이미지의 가로 길이인 $W_I$를 알고, $a_h$를 알면 우리는 이미지의 가로로 최대 몇 개의 사각형을 채울 수 있는지 알아낼 수 있다. 

단 사각형을 배치할 때 아래 그림과 같이 양 끝의 사각형은 이미지의 끝과 정확이 align 되게끔 배치한다.

 

 

만약 한 줄에 $q$개의 사각형이 배치되었다고 가정하면, 사각형의 중점 간의 거리는 총 $q-1$개가 생긴다.

 

그리고 가장 양 끝 사각형의 중점의 위치는 이미지의 가장자리로부터 각각 $a_h$만큼 떨어져 있기 때문에 특정 지을 수 있다.

 

그러면 이미지의 가로 길이인 $W_I$를 아래와 같이 나타낼 수 있게 된다. 

 

식 (1)

 

우리는 $W_I$를 이미 알고 있기 때문에 $q$를 구할 수 있는 식으로 변환하면 아래와 같이 나타낼 수 있다.

 

식 (2)

 

같은 방법으로 이미지의 세로를 채울 수 있고, 그렇게 되면 이미지의 높이인 $H_I$도 아래와 같이 표현할 수 있다.

이 때 $l$은 세로로 배치된 사각형의 개수이다. 

 

식 (3)

 

앞서서 정의한 영역의 수 $m$은 $q$와 $l$의 곱으로 나타낼 수 있다.

 

$m = q * l$ 이므로, $l = m / q$ --- (4) 이다. 

 

 

(3)식에서 l을 (4)로 대체하고 q를 (2)로 대체하면 아래와 같은 식이 된다. 

 

식 (5)

 

 

(5)식은 $a_h$에 대한 2차방정식으로 2가지 해를 갖는다. 

2개의 해 중에 하나는 항상 음의 값을 가지므로 나머지 하나의 값이 $a_h$에 해당된다. 

 

식 (6)

 

 

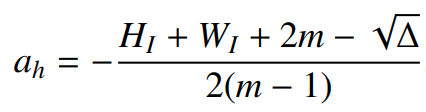
이 때, 식(5)의 판별식은 아래와 같이 간략하게 치환해서 나타내었다.

 

식 (7)

 

 

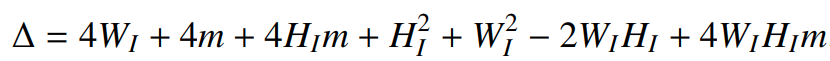
$m / q$ 의 값이 정수인 $ㅑ$에 대입되는 연산과

$a_h$의 값이 pixel 단위이기 때문에 버려지는 소수점 이하 값들이 있어서 

위의 solution을 통해 얻는 최대한 많은 영역의 개수인 $m$과 실제로 얻어지는 값은 정확하게 일치하지 않을 수도 있다.

 

 

SDC (Suppression vis Disk Covering)과 유사하지만, SDC는 $a_h$의 upper bound를 이미지의 길이($W_I$)로, lower bound를 1로 설정하였다. 

 

하지만 해당 논문에서는 이 $a_h$의 값을 좀 더 빠르게 구할 수 있는 방법을 제시한다. 

 

이 논문에서는 lower bound는 search boundary 분포가 가장 worst case인 경우에 해당함에 착안하여 lower bound를 아래와 같이 analytic 하게 설정해 주었다.